 |
 |
|
|
哥德巴赫猜想的证明
哥德巴赫猜想:任何一个不小于 6 的偶数都可以表示为两个素数之和。
只需证明不小于 6 的偶数这个概念与两个素数之和这个概念等价。概念是对一个事物的描述,包括事物的特征和实质,例如铜与金,特征是黄色重金属,实质是金要比铜重得多。万事万物正是因特征(象)与实质的不同而形成了差别。显然,不小于 6 的偶数其象仍然是偶数 1~0 (二进制,不含 0 )的象,只是实质少于偶数这个范畴;两个素数之和为偶数,象与前者相同。我们需要证明的是二者实质也相同。
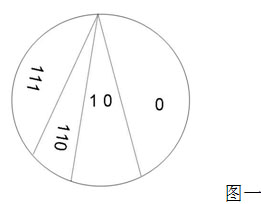
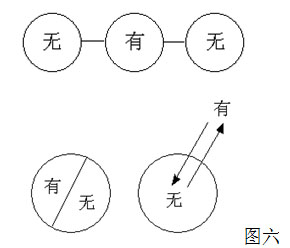
在一个有限的范畴(空间)中,要容纳无限的象,这些象有一种自然的分布规则,那就是象越细分,其所占的空间越小。例如在偶数这个空间,都是 1~0 的象,随着数值越大,象的表达越繁琐,所占空间也越小。这个空间的分配是每个象存在的条件,我们把这个空间的大小定义为象值。如图一:
这里涉及到一个有 / 无之象的空间分配问题,也就是一个实面和一个虚面之象在实质上的差别体现。
这要从一个实点和一个虚点谈起,宇宙是怎么来的?穷其本始,必然先有此象:
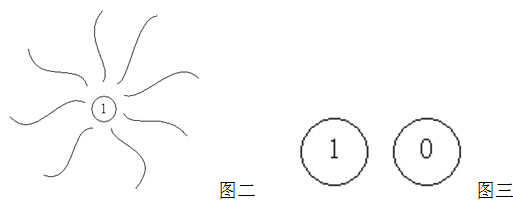
图二, 0 表示虚空, 1 表示最初的有。图三,定义此 1 为 1 个实点,定义占据 1 个实点同样的虚空为 1 个虚点,这个实点与虚点就出现了 1 个 1 与 1 个 0 的现象差别,也就是 11 与 10 的差别。而对 0 作 1 个的标记,是把虚空再进行了一次 1 、 0 的分割,这个 10 是在二分基础上的 0 ,这个 11 也是在二分基础上的 1 ,而此 11 比 10 多 1 ,故这个 10 的实质是 2 , 11 的实质是 3 。就这样产生了实点与虚点。实点累积在一起构成实体,虚点累积在一起构成虚空,世界就开始了形成。这就是老子所说的道生 1 (太极), 1 生 2 (虚无), 2 生 3 (实有), 3 生万物。老子说:万物皆生于有,有即 3 ,有生于无,无即 2 ;有名万物之母,无名万物之始,同归于玄,玄即本初的 1 ,玄之又玄,众妙之门。真正的 1 不可见,是真正的无象,可见的是 3 与 2 ,显示出 1 、 0 的表象。这个 1 就是道,先天地而存在。先筑 2 之虚空,再孕 3 之实有。这个 1 虽不可见,却非空非有,即空即有,不落空有两边。若问此 1 何来,佛说:无所从来,也无所去。 现在我们知道了一个实点与一个虚点成立的条件是 3 与 2 。形象是由实点构成的面(又名为有)与虚点构成的面(又名为无)共同组成的。如图四:
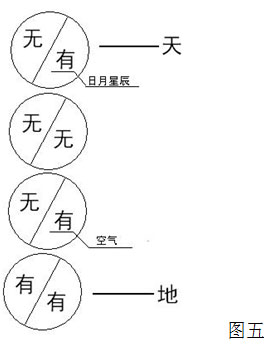
有与无必有分界线。这个界线就当二者兼备,既为实点,又为虚点,而且还要与实虚之象有所不同,处于一种中立状态却又无象。故此界线为 3 、 2 交合之状,其实质为 5 , 3 、 2 之差为 1 ,故表现为 1 之无象。实面表现为 3 之实象,虚面表现为 2 之虚象,界 5 是虚实之间的差别,因此实面的实质是 15 ,虚面的实质是 10 。古人形象地描述出我们这个世界的规则,如图五:
因此古人说天数 25 ,地数 30 ,天地之数 55 成河图之体,中间之数 45 成洛书之用,成变化而行鬼神。
从以上我们知道了有 / 无之象的分别其实质前提是 15 : 10 ,也就是说在图一的范畴二者进行分配时面积为 3 : 2 。我们来推导不小于 6 的偶数其象值是多少。 偶数 1~0 、奇数 1~1 (不含 1 )相当于对等的两个有象,故都赋予 15 的象值。偶数包含了 1 (有象 / 无象) 0 二种状态,有与无的比值是 3 比 2 ,于是 1 (无象) 0 也就是数 2 的象值为 6 。 1 (有象) 0 又可均分为二种状态, 1 (有象 / 无象) 00 与 1 (有象 / 无象) 10 ,分 9 为各 4.5 。 1 (无象) 00 也就是数 4 的象值为 4.5 乘 5 分之 2 为 1.8 。故偶数中去除 2 、 4 之后的象值为 15 减 6 减 1.8 ,为 7.2 。这就是不小于 6 的偶数这个概念的象值。
时间是什么?时间是在空间上发生的从无到有,又从有到无的这么一种从出现到消亡的变化现象。如图六:
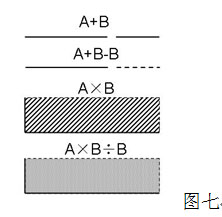
当有遮覆无时,名为有,当有离开之后,名为无。就这么一个过程,产生了一个 15 与 10 的分判。 10 一直在那里未变,那么属于变动的就是 15 。故时间也是一种实有之象。我们为何看不见它的形状呢?因为它分段来去,我们只能感受到它的一个片断。它的存在体现在物象的动态变化上。 古人把因为时间带来的物象变化过程(如春夏秋冬)表示为加减乘除四种状态,代表渐增、渐减、暴增、暴减,其数分别为 8 、 7 、 9 、 6 。如图七:
加减是一种时间现象,实线出现了,又消失为虚线。乘除也同样,实面出现了,又消失为虚面。故都以时间之值 15 分为二段。这二段有何不同?一个是出现实线与出现虚线的差别,一个是出现实面与出现虚面的差别。一个实面与一个同样的虚面有 15 比 10 的关系,又因总值为 15 ,故分为 9 、 6 。实线与虚线则与界发生了关系,界值为 5 ,实点为 3 ,虚点为 2 ,总值 15 ,故分为 8 、 7 。 或者从分拆和连接角度来看,如图八:
在分拆时,要出现一个虚点,数为 2 ,原本这是一个实点,数为 3 ,因此同样的线条处于连接状态要比处于分拆状态多 1 ,总体是 15 ,故连接时是 8 ,分拆时是 7 。 加减乘除四种变化状态对应的数为 8 、 7 、 9 、 6 ,这是四象出现的实质条件,物象在变化时整体被分割显示成 8/15 、 7/15 、 9/15 、 6/15 四种长消盈亏状态。 8 、 7 、 9 、 6 是一个实面 15 之物象发生相应演变之象值。
奇数是一个范畴 ( 空间 ) ,素数是对这个范畴的分割,是对空进行了标注,从而区分哪些是素数,哪些是非素数。也就是说有一个象 ( 或者说信息 ) 进驻此空,而作标注。是什么象进入导致分化?每个奇数都或者是素数,或者是素数以乘法之象相联。在奇数之下,除了素数 / 无就是素数 / 有乘法之象;或者说本来是无,其中有些加载了乘法信息的标记,而区分出素数与非素数。就象都是人,有钱或无就分出了富人与穷人。这个进驻的信息就是乘法。如图九: 对于一个本来是无的空间即虚面 10 而言,乘法的象值为 9 ,也就是说,有 10 分之 9 的空间弥漫着其信息,而无只龟缩在 10 分之 1 的空间里。 由于象与象值存在一定空间的反比关系,譬如,沙子的数量巨大,金子稀有,于是沙子便宜、金子昂贵。如图十:
B 象值相当于 A 象没有占据的虚空,记住- A 象; A 象值相当于 B 象没有占据的虚空,记作- B 象;就虚空而言,两者仍然是一个 A 象和 B 象的对比。两个象与象值在同样的范畴里存在反比的分配关系,如同名与实的关系一样。 因此对于与图九相对应的一个实面而言,素数则占据 10 分之 9 的空间。为何?譬如:当我们知道了 9 成地域的人要被财富奴役,或者说 9 成的财富属于富人,就可直接推导出穷人占 9 成。 与偶数 1~0 之实面 15 对应的是奇数 1~1 之实面 15 。故而素数的象值为 15 乘以 10 分之 9 ,为 13.5 。
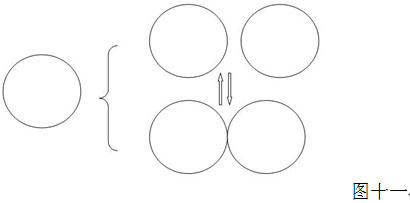
根据象与象值的反比原理,如果一个实面 15 之象复制成为两个,如图十一:
则两倍面积的象其象值只有一半 7.5 ,由于这个象在连接与分拆时有 1 的差别,故分拆状态象值为 7 ,连接状态象值为 8 。
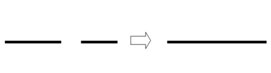
两个素数的和,相当于素数之象在分拆之后走向连接,如图十二:
这是一个加法的示意图,也是素数之象处于分拆、连接两种变动状态的示意。素数之象的象值为 13.5 ,故分拆状态 7/15 象值为 13.5 乘以 7/15 ,连接状态 8/15 象值为 13.5 乘以 8/15 等于 7.2 。这与不小于 6 的偶数象值 7.2 完全相同,因此两个概念等价。命题获证。
以上的推导是一种象数思维,有些地方跨度较大,不易理解。象数学是形而上的哲学基础,是我国古代一切学问的根本。朋友建议我在此基础上建立一个完整的数论,然后逻辑严密地对猜想予以证明。我回答说自己已经穷尽了心力,这件事就留给后人去做吧。牛顿发明了微积分,但是理论基础直到极限学说出现才得以完善,“尚有待于来者” ……
|
 图二
图二 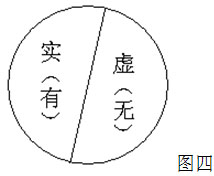
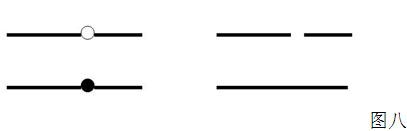

 图十二
图十二